介绍

英文题目：Unsupervised Knowledge Graph Alignment by Probabilistic Reasoning and Semantic Embedding

中文题目：基于概率推理和语义嵌入的无监督知识图对齐

论文地址：https://arxiv.org/abs/2105.05596v1

领域：自然语言处理，知识图谱

发表时间：2021

作者：腾讯天衍实验室

出处：IJCAI（国际人工智能联合会议）

被引量：1

代码和数据：

https://github.com/qizhyuan/PRASE-Python

https://github.com/dig-team/PARIS

阅读时间：22.04.08

泛读

针对问题：实体对齐（不是本体对齐）
结果：效果优于之前模型
核心方法：提出 PRASE，基于概率推理和语义嵌入，使用不断更新种子的方法迭代训练上述两个子模型。
难点：先需要了解一下 PARIS 模型
泛读后理解程度：70%

（看完题目、摘要、结论、图表及小标题）

精读

摘要

目前常用的实体对齐方法包括：基于词嵌入的对齐、常识推理和字典匹配。前者的模型常常依赖有监督学习，缺乏恰当的推理，难以避免逻辑错误的映射；后者解决了推理问题，但较少使用图结构和实体上下文。本文致力于结合二者。

1. 介绍

实体对齐可用于把局部的知识图结合成更大的知识图，具体的工作是需要找到不同图中含义相同的实体、关系等。

图嵌入将图中实体关系等信息编码到低维空间，使其包含的语义信息作为进一步探索的工具。对齐问题的解决方法常常是：先将待对齐的知识图嵌入到一个向量空间中，然后通过计算向量距离或相似性来发现映射。

这些基于嵌入的模型常常需要一定数量的知识映射（对齐种子）来进行训练，而种子标注需要大量人力。种子的数量和抽样分布对对准性能有很大影响。而且先编码后映射的方法可能忽略整体性，从而导致映射错误。

使用逻辑推理或者字典映射，本体对齐方法是相对传统的技术，比如 2012 年的 PARIS 利用概率归因和字典映射方法，通过名字匹配一些初始特征之后，通过迭代概率推理来推断实体、关系的等价性。因此无需训练，不依赖种子，更高效和可扩展。但它在开发和利用图形结构和其他上下文信息方面较弱。

本文致力于结合上述两种模型，提出了无监督的迭代框架 PRASE。其中的 PR 是概率推理模块（probablistic reasoning），SE 是词嵌入（semantic embedding）模块。PR 基于之前 PARIS 模型，SE 用于捕捉图结构和实体的上下文，PR 从 SE 处得到映射和实体嵌入。

本文主要贡献如下：

提出无监督的对齐框架 PRASE，用迭代方法结合了两种模型
使用 PARIS 和不同的词嵌入模块实现模型
在多个数据集上达到比之前更好的效果

2. 预备知识

背景和相关工作

2.1 问题表述

设符号：E 是实体，R 是关系，A 是属性，V 是属性值。将图定义为 G=(E,R,A,V,TR,TA)，其中 TR 指关系三元组，TA 指属性三元组：

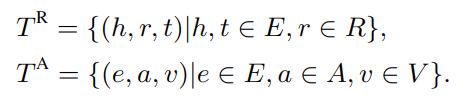
问题定义成对两个图 G 和 G' 中实体的对齐方法：

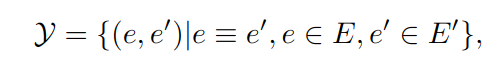
"≡" 指的是两个实体指向现实世界中的同一对象。

2.2 PARIS 方法

属性三元组和关系三元组类似，因此定义：

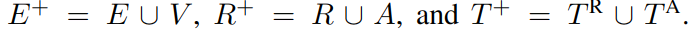
并且定义了关系的度量函数及其反向函数：

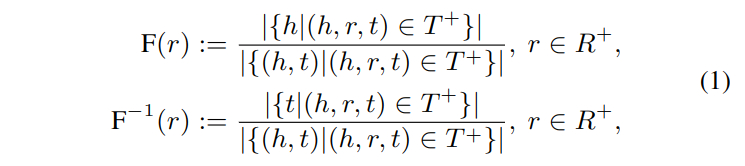
其中|.|表示集合的基数（集合中的元素数量），上述函数用于计算头实体和尾实体的唯一性。当 F(r)=1 时，说明其头实体是唯一的，请注意：F 和 F-1 具有不变性，因此，可提前计算。

PARIS（2012 年论文，用于对齐实例、关系、类，适用于大型图）可以交替计算实体映射和包含关系，不同图中的两个实体 h 和 h' 相等的概率 P(h ≡h′)，计算如下：

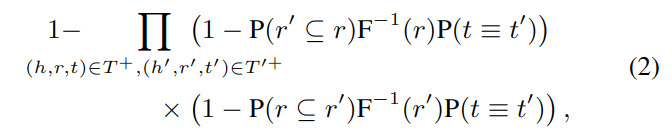
其中 (h,r,t) 是图中的三元组，式 -2 的大概意思是：在确定了尾实体相等的概率、关系 r 的逆函数 F-1，以及 r 与 r' 包含关系的概率后，即可计算头实体 h 与 h' 是同一实体的概率。

其中 P(r ⊆ r′) 表示 r 是 r' 子集的概率：

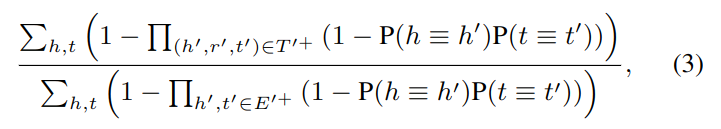
式 -3 假设已知头实体和尾实体分别指向同一实体的概率，分母计算所有 h,t，分子计算包含 h,r,t 的三元组。

可以看到计算 P(r ⊆ r′) 需要 P(h ≡h′)，而 P(h ≡h′) 又需要 P(r ⊆ r′)，二者相互依赖，因此需要迭代优化。一开始，P(r ⊆ r′) 可被设置为一个很小的值，比如 0.1；或者，当实体是属性时，如果文字描述相同则设为 1，否则为 0；更高级的方法是用实体间的编辑距离作为其评分。

在每次迭代时，式 -2 计算出了实体相等的概率，式 -3 又计算了关系的包含关系，迭代直至收敛。最终 PARIS 输出的是实体映射表记作 ̃YP，Po(e≡e‘)，(e，e’)∈Yp，上标 o 表示输出。

2.3 基于嵌入的知识图对齐

基于嵌入的知识图对齐一般分两步：先学习词嵌入（如使用 TransE 或图神经网络），在不同图中使用同一向量空间编码，通过参数共享、参数互换、嵌入变换、嵌入校准等策略实现；然后，基于度量实体嵌入的相似性来预测实体映射。

MTransE 是比较典型的嵌入方法，通过以下损失函数优化：

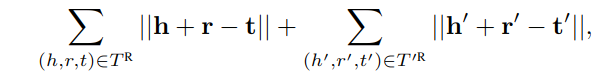
其中||.||计算欧几里得范数，h,r,t 都是编码后的低维向量，处于同一向量空间。一般情况下需要种子训练模型：

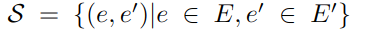
最小化损失：

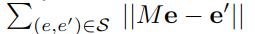
其中 e 和 e' 是实体嵌入，维度为 m，M 是大小 mxm 的转移矩阵。通过学习 M，G 可被转换到 G' 所在的空间。最终实现实体映射记作 ̃YE，其相似度在[0,1] 之间。记作: S(e ≡ e′),(e,e′) ∈ ̃YE。通过该方法可以进行近邻搜索。

3. 框架

3.1 PRASE 概览

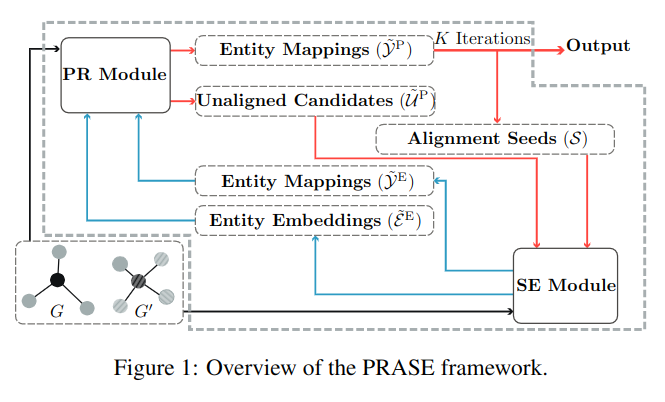
模型框架如图 -1 所示，主要由概率模型 PR 和嵌入模型 SE 组成。PR 用于计算实体映射 ̃YP 及其概率 Po。然后将高置信度的映射作为种子，传入嵌入模型 SE，SE 通过这些种子来训练模型，然后 SE 模型对于 PR 模型输出的未对齐的实体 ̃UP 进行预测；之后，将 SE 预测结果实体映射表 ̃YE 和相似度得分 S(e ≡ e′)，以及实体嵌入结果：

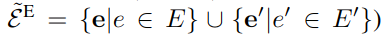
作为 PR 模块的输入，再进行下一次迭代。以上过程迭代 K 次，PR 模型最终输出实体映射表 ̃YP。

3.2 概率推理模型

PR 模块首先利用式 -1 计算出关系的函数 F 及其反向函数，然后利用式 2 式 3 计算两个实体的相似概率。PR 与 SE 交替调用，在 k 次迭代时（k>0），将前次输出作为本次的输入

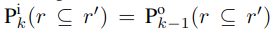
i 指输入，o 指输出，每次迭代时 PR 的输入如下：

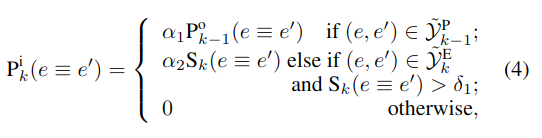
P 指的是 PR 模块的映射概率。当前一个 PR 模型认为两实体对齐时，将其为同一实体的概率以权重 a1 代入；当 SE 模型认为二者对齐且相似度大于阈值δ1（δ1,a1,a2 均为超参数，取值范围在 0-1 之间），将其相似度以权重 a2 代入；否则设其概率初值为 0。

为了更直接地利用 SE 输出的嵌入信息，在迭代过程中，将 PARIS 中的式 -2 变为式 -5：

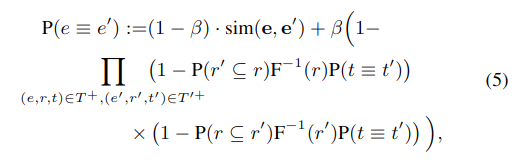
利用超参数β（取值 (0,1)）来平衡词向量相似度和 PARIS 计算的概率。sim() 计算 cosine 距离，其取值在[0,1]。

3.3 语义嵌入模块

在第 k 次迭代时，利用上一次 PR 产生的对齐数据集 Yk-1，从中提取出置信度高（超参数δ2 作为阈值）的对齐数据作为种子 Sk 来训练 SE，尽管很多时候种子中包含不正确的数据，但是它也能带来大量的有用信息。用训练好的 SE 代入未对齐的实体 U，它将输出与 U 最相似的实体，以及词嵌入。任何词嵌入方法都可以用作 SE。

PRASE 流程如算法 -1 所示：

对于两个图 G 和 G'，设置迭代次数 K。

line 1：用式 -1 初始化 PR 模块（通过两图中三元组计算关系函数 F）

line 2：PR 处理：用式 -2 和式 -3 依次计算实体相似概率和关系的包含

line 3：产生了初始的对齐数据集 Y0 和未对齐数据集 U0。

line 4：开始迭代

line 5：基于前次对齐数据集 Yk-1 产生种子

line 6：使用种子训练 SE 模型

line 7：用 SE 模型对前次未对齐数据 Uk-1 预测

line 8：产生了本次预测结果 YE 和嵌入结果 EEk

line 9：使用式 -4 初始化 PR 模型

line 10：PR 处理，计算式 -5 和式 -3

line 11：产生了本次的对齐数据集 Yk 和未对齐数据集 Uk。

line 12：继续迭代

line 13：最终输出 Y

4. 评价

4.1 数据集

OpenEA 数据集：常用的用于评测图对齐的数据集。由 DBpedia, YAGO, and Wikidata 组成，文中评测使用其 V2 版本，包含跨语言数据集和跨知识图谱数据集，另外，还使用了相对困难的数据集 D-W-15K-V2。

下载地址：https://github.com/nju-websoft/OpenEA

工业数据集：MED-BBK-9K 是 Zhang 在 2020 年提出的数据集，包含专业医学数据集和百度百科医学数据（中文），约几十万个三元组。形如：

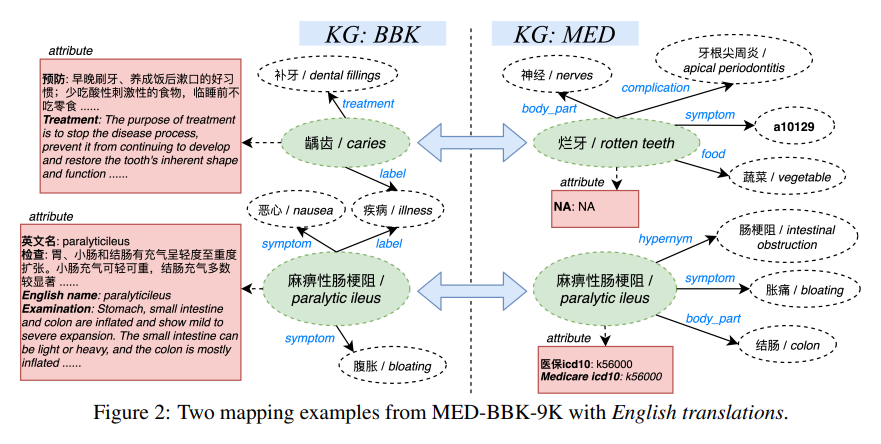
下载地址：https://github.com/ZihengZZH/industry-eval-EA

解压后即可看到三元组数据（又解锁一个中文的医学图谱数据及其对齐算法，开心）。

4.2 实验设置

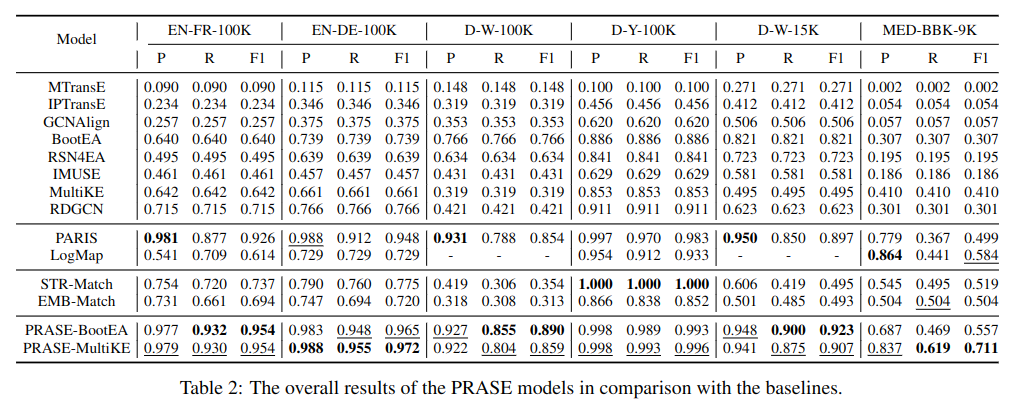
最上边部分是嵌入模型，第二部分是推理模型，STR-Match 和 EMB-Match 计算实体间的相似度，最后一部分是 PRASE 模型分别使用 BootEA 和 MultiKE 模型作为 SE。

实验环境是：NVIDIATesla M40 GPU, and CentOS 7.2，128G 内存，2.4GHz CPU。对于 4 个 100K 的数据集的训练速度是平均 1697 秒，BootEA 和 MultiKE 分别是 24727 和 3198。

表 -3 和表 -4 分别展示了消融实验和不同嵌入模型的对比效果。

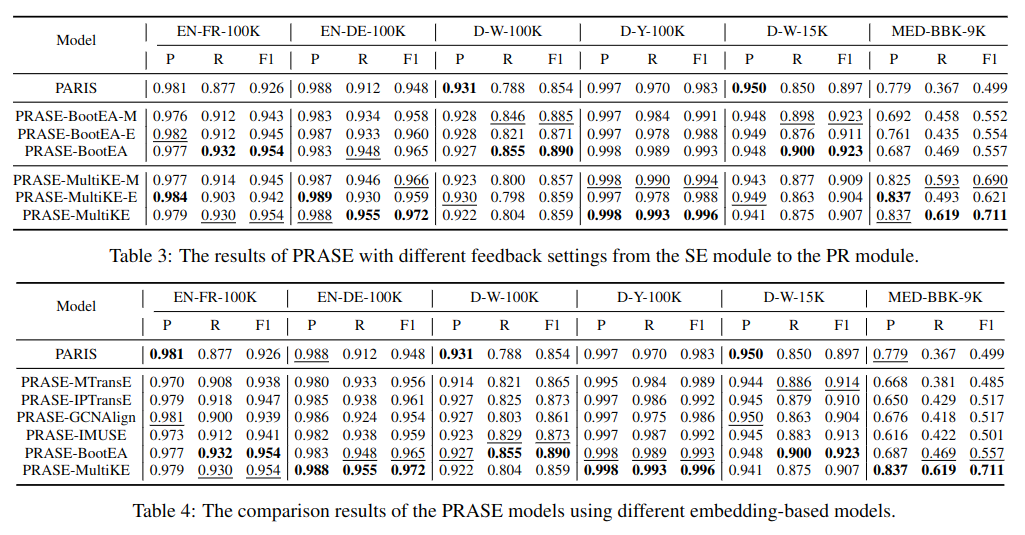
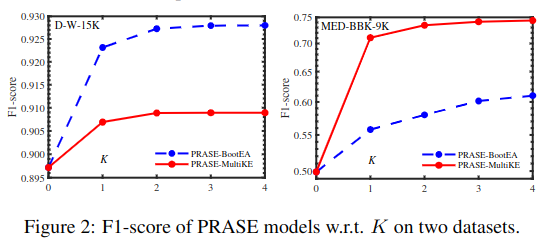
图 -5 展示了不同迭代次数对模型的影响，更多的迭代可以提升模型效果，但 K 也不用设得太大。

PRASE-Python 代码解析

下载

$ git clone git@github.com:qizhyuan/PRASE-Python.git

运行

$ PRASE-Python/

$ python test.py

（程序在我笔记本 CPU 环境下运行时间约 2 分钟）

代码

test.py 测试程序
objects/KGs.py 最核心代码
objects/KG.py 图数据结构支持
objects/Entity.py 实体数据结构支持
objects/Relation.py 关系数据结构支持
model/PARIS.py 概率推理模型

代码没有用什么特殊的库，在任何 Python 环境里都可以运行。

数据集

介绍

论文中测试了多个数据集，代码中包含了对 Wikidata 和 dbpedia 两个知识图的对齐，以便跑通测试程序。具体使用的是 D_W_15K_V2，包含 15K 个实体的版本 2。

所需数据

data/*

三元组：
- 二个图的属性三元组 attr_triples_1, attr_triples_1
- 二个图的关系三元组 rel_triples_1, rel_triples_1
实体关系：ent_links
嵌入模型结果：其中包含对齐结果，实体嵌入，关系嵌入等
- BootEA/* 实体嵌入训练结果
- MultiKE/* 实体嵌入训练结果

分析

结合论文再看数据集就非常真观，嵌入模型，比如 MultiEA 输出由两部分组成：实体对齐结果&实体嵌入。

代码细节

针对 KGs.py 分析，代码包含两上类 KGs 和 KGsUtil，前者保存图对齐过程中的数据和逻辑；后者为辅助工具，一方面用于存取数据，

sub_, sup_ 分别是论文中提到的两个包容关系。

ent_match, ent_prob 分别是实体匹配关系及其概率

注意

代码中没有更新 SE 模块的部分，主要以实现 PARIS 的 Python 版本为主，github 的 README 最后也提到（截至目前 2022.04.14），如果想更新 SE，需要和其它工具配合，比如 OpenEA。

如何代入自己的数据

先用自已的数据训练词嵌入
然后参考 data 下的数据格式做数据后，即可训练

收获

这是一个非常好的示例，之前我们拿到各种格式的异构图都可以照葫芦画瓢地训练一波。

目前为止，对图的认识是：

无论原理还是算法都没那么复杂；
能把支持各种无法统一的数据，转换成嵌入的数值；