论文阅读_近端策略优化_PPO
1 | name_ch: 近端策略优化算法 |
读后感
PPO 近端策略优化是一种强化学习算法,具体是对深度学习策略梯度方法的优化。
策略是强化学习中用于决定在每个时刻采取哪个动作的函数。 近端约束用于限制策略的变化,以避免过于激进地改变策略。
文中介绍了两种方法:截断和 KL 散度,近端约束通常使用梯度截断来实现,即将梯度限制在一个特定范围内,让学习的步调不要太大。
介绍
一种改进版的强化学习策略梯度算法。它从与环境交互的数据中采样。不同于标准的策略梯度方法对每次采样执行一次梯度更新,文中提出了一个新的目标函数,可以实现多个 epoch 的 minibatch 数据更新,另外,它是 TRPO 的改进算法,相对 TRPO 更为简单,InstructGPT 的强化学习用的就是 PPO(ChatGPT 可能也是)。
方法
优化算法
文章介绍了三种方法,其差别主要在损失函数,公式如下图所示:
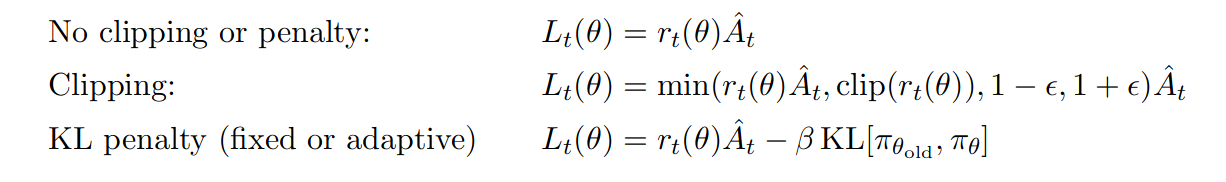
第一种方法的目标是对神经网络 theta 调参,其中 L 表示损失 Loss,At 是时间步 t 的优势函数,注意这里的 r 不是奖励,而是新旧策略的变化,当策略不变时 r=1:
\[ r_{t}(\theta)=\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)}, \text { so } r\left(\theta_{\text {old }}\right)=1 \]
第二种是本文中推荐的剪裁方法,它通过限制损失函数,从而限制了后续调参;其中 epsilon 是超参数,一般是 0.2,它将变化范围限制在 0.8-1.2 之间(上图是论文的截图,我觉得括号位置好像写错了)。
第三种是将KL 散度作为惩罚项加入了公式,以保证旧策略 pi_old 与新策略 pi 尽量相似,其中 Beta 是超参数,可以是固定的,也可以自动计算,文中还引入了一种自动计算 Beta 的方法,dtarg 为超参数,先根据当前状态计算 d,然后计算 beta:
\[ \begin{array}{l} d=\hat{\mathbb{E}}_{t}\left[\operatorname{KL}\left[\pi_{\theta_{\text {old }}}\left(\cdot \mid s_{t}\right), \pi_{\theta}\left(\cdot \mid s_{t}\right)\right]\right] \\ \text { - If } d<d_{\operatorname{targ}} / 1.5, \beta \leftarrow \beta / 2 \\ \text { - If } d>d_{\operatorname{targ}} \times 1.5, \beta \leftarrow \beta \times 2 \end{array} \] ### 具体实现
PPO 也属于一种 A-C 方法,即结合策略和价值的方法。为了同时优化价值和策略,设置最终的目标函数如下:
\[ L_{t}^{C L I P+V F+S}(\theta)=\hat{\mathbb{E}}_{t}\left[L_{t}^{C L I P}(\theta)-c_{1} L_{t}^{V F}(\theta)+c_{2} S\left[\pi_{\theta}\right]\left(s_{t}\right)\right] \]
其中 c1,c2 是超参数,用于设置各方占比;CLIP 指的是策略目标,即上面描述的裁剪方法;LV 是状态价值的差;优化的目标是最大化整体 L,所以对其中的 VF 项做减法;和 S 是熵奖励,用于增强熵,以确保充分的探索。
具体算法如下:

其中优化的点是:使用并行的 N 个 actors 分别收集 T 时间步的数据;然后针对 NT 数据,通过 K 次 epoch,用小批量数据 M 调整梯度,实验证明效果更好。
实验
三种方法对比效果如表 -1 所示:

其中 Clipping 在 epsilon 设为 0.2 时效果最好;对于 KL 散度方法,测试了通过 dtarg 自动计算 beta 和设固定 beta 两种方式,可以看到自动计算的方式略好。
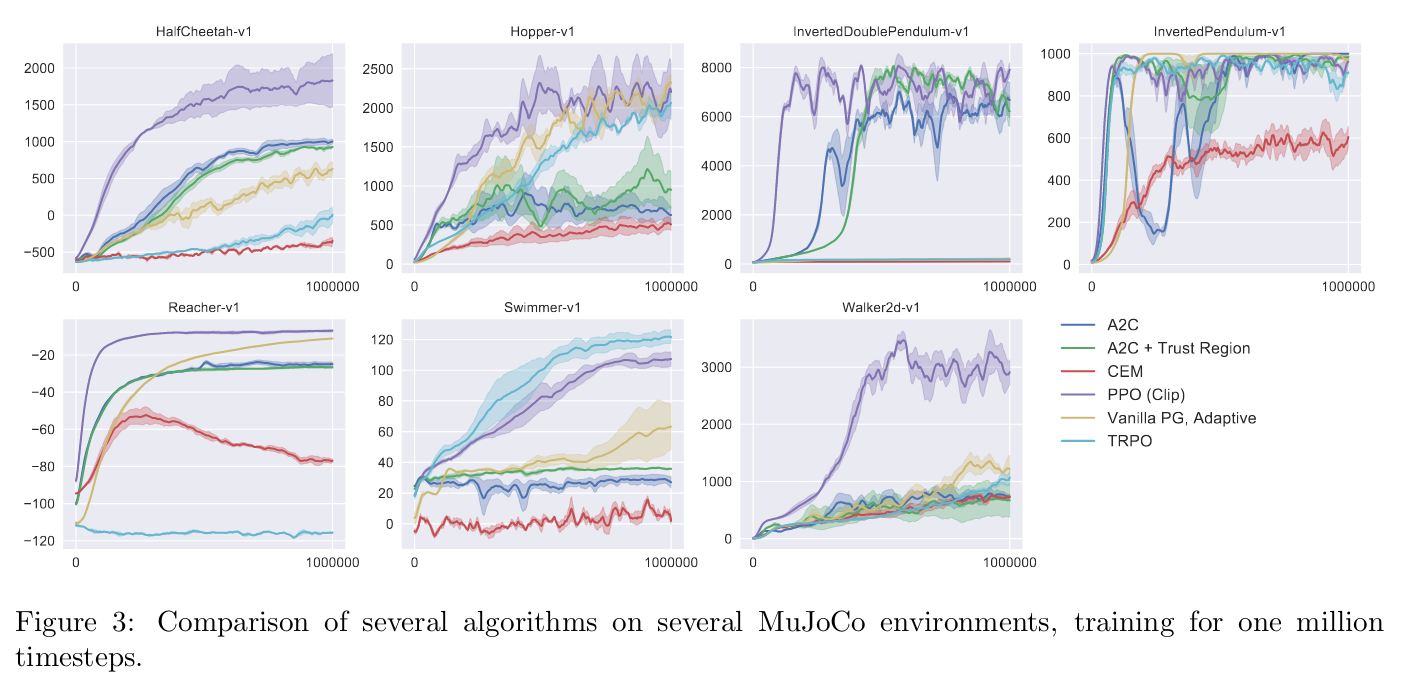
与其它强化学习相比,从图 -3 可以看到,在大多数任务中 PPO(Clip) 都优于其它算法。除此以外,实验部分还针对连续领域及 atari 游戏对比了 PPO 与其它算法的效果。
收获
- 这个剪裁挺好的,调得太过了,就剪掉
- KL 是比较分布,所以似乎更优美
