论文阅读_关系表征的在线学习DeepWalk
读后感
- 针对问题:学习图中节点的表征,解决多分类、异常检测等问题。通过优化算法,可应用于大规模数据。
- 结果:当标签数据稀疏时,F1 分数比之前方法提升 10%;在一些实验中,使用 60% 训练数据,结果即可优于其它方法。
- 核心方法:借鉴自然语言处理方法,利用统计原理,使用无监督数据学习。
- 难点:优化部分较难理解。
- 泛读后理解程度:直接精读。
(看完题目、摘要、结论、图表及小标题)
介绍
英文题目:DeepWalk: Online Learning of Social Representations
中文题目:DeepWalk:关系表征的在线学习
论文地址:http://perozzi.net/publications/14_kdd_deepwalk.pdf
领域:知识图谱
发表时间:2014
出处:KDD
被引量:5094
代码和数据:https://github.com/phanein/deepwalk/
阅读时间:2022.3.28
精读
1. 介绍
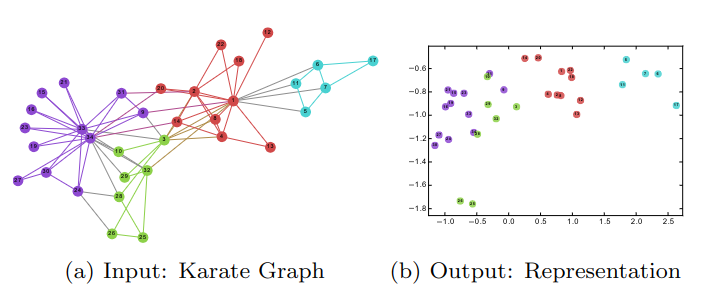
编码的目标是使用相对较低的维度表征数据,如图以 2 维为例,左图是输入,右图是输出,可以看到,输入中的连接关系,可表征成输出的特征的相似性,颜色表示它们的聚类结果。
把稀疏的表示转换为低维稠密表示之后,可以使用统计学方法建模,比如使用简单的逻辑回归算法进一步处理。
文章贡献如下:
- 提出 DEEPWALK 算法,使用深度学习方法分析图,构建适用于统计建模的健壮表示,利用短程随机游走学习图结构中的规则。
- 将文中方法应用于多标签的分类任务中,在稀疏问题上,有 5%-10% 的提升,在一些情况下可减少 60% 的训练数据。
- 文中展示了算法的可扩展性,可利用并行计算,应用于网络规模的图(如 YouTube),并通过较小的修改构建流式版本(online learning)。
2. 问题定义
设 G=(V,E),G 是图,V 是顶点,E 是边,GL=(V,E,X,Y) 是部分标注的图,其中 X 是节点的 S 维特征,Y 是标签。
传统方法是希望找到 X 与 Y 间的映射 H,而文中方法的目标是利用嵌入在网络结构中的节点相关性信息,实现更好的表征。
文中利用无监督方法,学习图中展示的结构特征,而非把标签作为特征的一部分,使得新表征与标签分布无关。
本文的目标是学习低维的 X 表征,每个维度表达一些概念。这些表征是相对通用的,与具体算法无关,可用这些表征解决下游的决策问题。
3. 学习关系表示
希望找到有以下特性的方法:
- 适应性:可适应网络的不断进化,而无需每次都从头训练。
- 社区意识:新表征的相似性应于网络中的相似性保持一致。
- 低维度:低维度的新表征,有更好的泛化性,训练和预测速度更快。
- 连续性:新表征中的特征是连续值,从而实现更强的健壮性。
3.1 随机游走
从节点 vi 开始,随机访问 \(W_{v_i}^1,W_{v_i}^2...W_{v_i}^k\),\(W_{v_i}^{k+1}\) 是随机从 vk 的邻居中选择的顶点,简单地说就是 a 到 a 的邻居 b,b 再到 b 的邻居 c……随机游走已被用作内容推荐和社区检测等应用中,用于度量相似性。用它计算本地结构信息,时间上与输入图的大小呈次线性关系。
文中使用短程随机游走作为工具从网络中抽取信息,它提供了两种特性:可使用并行方法来探索图中的不同部分;小的改变不需要对全图重新训练。可以迭代更新模型,时间上是次线性的。
3.2 连接:幂律
如果连接图中度的分布满足幂律,短程随机行走中顶点出现的频率也将服从幂函数分布。
幂律 (Power Laws) 指的是:节点具有的连线数和节点数目乘积是一个定值。
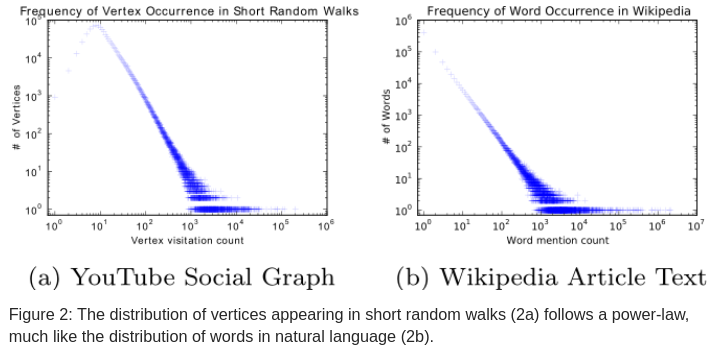
自然语言中的词频与图中节点的随机游走分布类似,如图 -2 所示,左图是 YouTube 网络中短程游走情况,横坐标是节点出现的次数,纵坐标是节点数量,也就是说只有少量节点游走的次数很多;它可类比成自然语言处理如右图,Wikipedia 中常用词非常少。本文将一些自然语言建模技术用于图的建模。
3.3 语言模型
自然语言模型的目标是估计由单词组成字符串的正确性。对于单词 (w0,w1,...,wn),利用训练集,最大化概率 Pr(wn|w0,w1,...,wn-1),具体方法是使用概率神经网络泛化成词表征。
解决图问题时,相应地使用短程随机游走,把游走视为语言中的短语或短句,根据之前节点关系,预测下一节点 vi
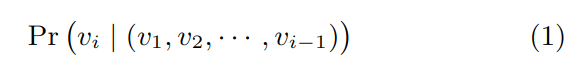
文中目标是不仅学习节点共现的概率分布,同时生成一种映射关系Φ,将网络中的关系表征为节点 d 维向量,然后用它进行后续计算。
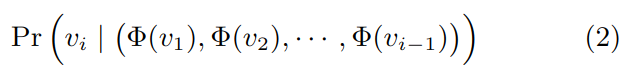
随着随机步数的增加,条件概率计算量则变得非常大。
在自然语言问题中,最近提出一些新的算法:将通过上下文预测缺失词,改为通过一个词预测上下文;上下文由其左右两侧词组成,改为不考虑上下文中词的顺序,只最大化上下文中词出现的概率。对节点表示问题,也可做相应优化:
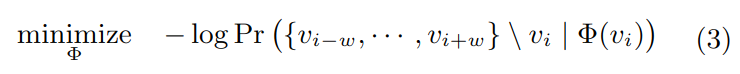
(上式中斜线的意思是除 vi 以外)
顺序无关性能更好地捕捉到随机游走中“近距离”的节点,另外,一次给出一个顶点构造小模型,也加快了训练速度。
式 -3 中捕捉了本地图结构中共享了相似性,具有相似邻居的节点需要近似的编码表征,也可泛化到其它机器学习任务中。
4. 方法
4.1 概述
自然语言建模时需要语料库和词表 V,DEEPWALK 将截断的随机游走看作语料库,将图中节点看作词表。
4.2 算法:DEEPWALK
算法主要包括两部分:产生随机游走;更新程序。过程中以每个节点 vi 作为起点进行游走 Wvi,游走从最后访问的顶点的邻域均匀采样,直到达到最大长度 T。

外层循环游走整体的迭代遍数(一共试着走几次),在每次遍历开始时,第 4 行生成一个遍历顶点的随机顺序,这样做能加快随机梯度下降的收敛。
内层循环遍历图中所有节点,对每个节点产生 t 步的随机游走 W(随机游走的路径和长度都是随机的),在第 7 行使用它代入 SkipGram 算法来更新表征,其目的是优化式 -3 中的目标函数。
4.2.1 SkipGram
参见:[[2_Note/0_Technic/2_算法/6_自然语言/Embedding/几种词嵌入方法#Word2Vec的skip-gram模型]]
SkipGram 是一种语言模型,它在句子中设置窗口,然后计算窗口中词的最大共现概率。对于式 -3,在假设词相互独立的情况下,概率可表示成乘法关系:
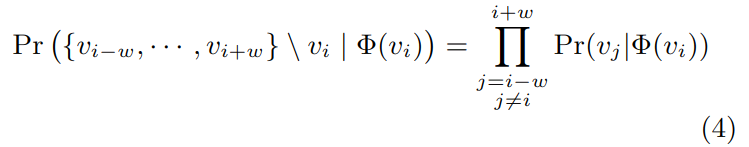

算法 2 遍历了在窗口 w 中随机游走的所有可能性,将 vj 映射成新表征Φ(vj),最大化游走到它邻近节点的概率,J 是目标函数,通过它来优化Φ。
4.2.2 分层 Softmax
(这部分比较难理解,我试着扩展一下,可能不对)
算法 2 中第 3 行,当图中节点较多时,计算量非常大。因为 Softmax 归一化,要计算图中所有的节点。因此文中提出了分层 Softmax,实际上是把多分类变成了二分类树,即把 softmax 变成了多次 sigmoid。
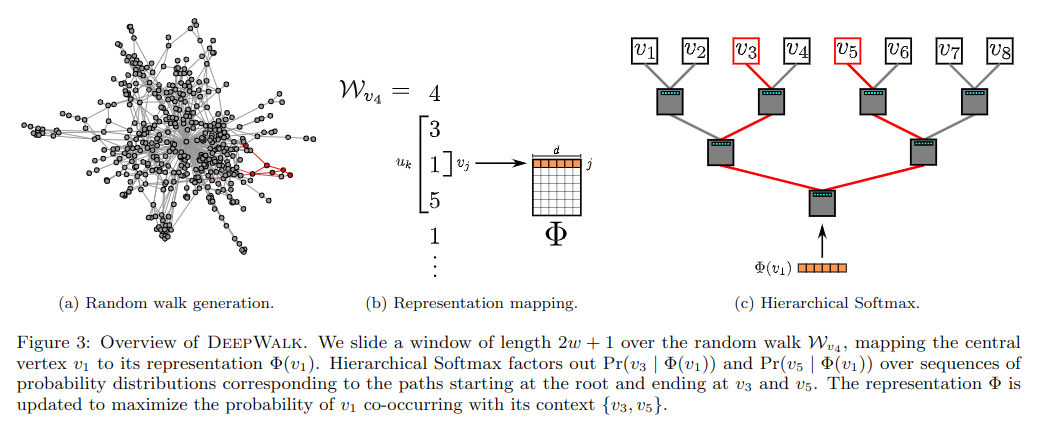
如图 -3(c) 所示,用与 v1 相关的节点作为叶子,构造了一个二分类树,从而把预测问题变成最大化树中特定路径的概率问题。当从起点到 uk 的路径被认为是经过一系列树节点 b(b0 是根节点,\(b_{[log|v|]}=u_k\)),则有:
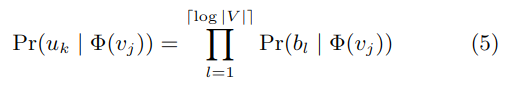
此时的 Pr 被构建成二分类器(sigmoid 函数):
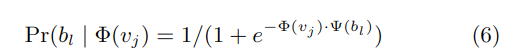
其中Ψ(bl) 是 bl 父节点的表征,它把复杂度从 O(|V|) 降到了 O(log|V|),从而加速了训练。
为加快训练,在构造树的过程中,给随机游走中通向频繁顶点的过程分配较短路径,使用哈夫曼编码来减少树中频繁元素的访问时间。(简单地说,就是先判断可能性最高的,从而减少判断次数)
4.2.3 优化
计算模型参数θ = {Φ,Ψ} 的时间复杂度是 O(d|V|),算法 -2 第四行使用 SGD 方法优化参数。学习率初值是 2.5%,逐步减少。
4.3 并行
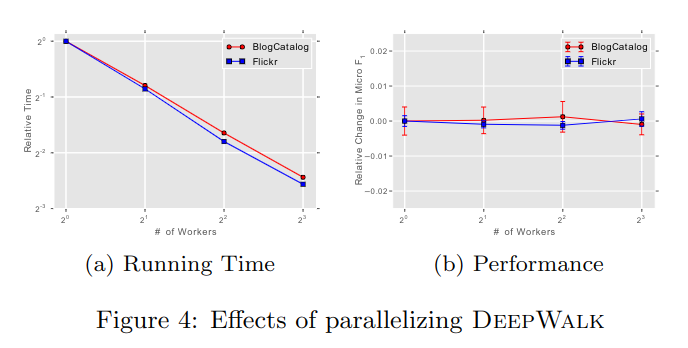
图 -2 展示了随机游走的频率分布服从幂律,这导致了低频顶点的长尾分布,Φ的稀疏性使我们可以使用随机梯度下降的异步版本 ASGD,并行计算,且不需要加锁。它可被扩展到大规模的机器学习中。图 -4 展示了并行计算的效果,可以看到随着线程数的增加,训练时间变短(左),且模型精度变化不大(右)。
4.4 算法变异
4.4.1 流方法
流式方法在不需要了解全图的情况下也能计算,变化是游走直接更新模型。具体修改是:不再使用学习率衰减,而是将其设定为一个小的常数,因此,需要更长的时间学习;另外,不再需要建立树的参数。
4.4.2 非随机游走
有一些图通过交互产生,比如用户在网页中导航。这种情况下就不需要随机游走,可以直接用路径建模。这样采样不仅与网络结构有关,还包含了路径的频率。
结合上述方法,可以持续改进网络,而不需要确定所有信息后再构建整个网络。这种方法可以用于处理大规模网络。
5. 实验设计
5.1 数据集
- BlogCatalog:由博客作者相互关系构建的网络,标签是作者的主题类别。
- FLICKR:图片共享网站用户之间的联系人网络,标签是用户感兴趣的组。
- YOUTUBE:视频用户关系网络,标签是喜欢同一视频风格的群体。
5.2 基线
- 频谱聚类:使用拉普拉斯矩阵的前 d 维特征向量作为表征,然后对表征聚类。
- 模矩阵:使用图 G 的模矩阵 B 的前 d 个特征向量表征。
- 边聚类:对邻接矩阵使用 K-means 聚类。
- wvRN:根据领居权重投票方法。
- 少数服从多数:简单地选择训练集中出现最多的标签作为类别。
6. 实验
6.1 多标签分类
6.1.1 BlogCatalog
分别使用训练集的 10%-90% 进行训练,可以看到 DEEPWALK 优于频聚类以外的其它方法,当标注少时,DEEPWALK 比频聚类更有优势,这是文中算法的特点。
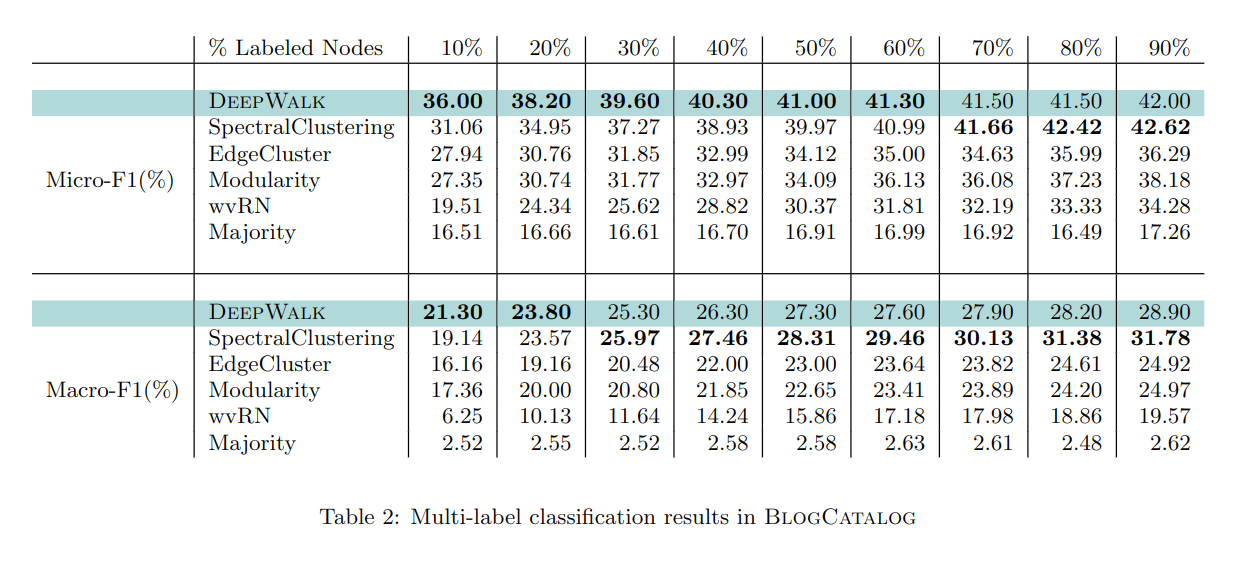
6.1.2 Flickr
实验分别标注了 1%-10% 的数据,可以看到 DEEPWALK 优于其它算法,它只需要 60% 甚至更少的数据,就能达到与其它算法相同的精度。
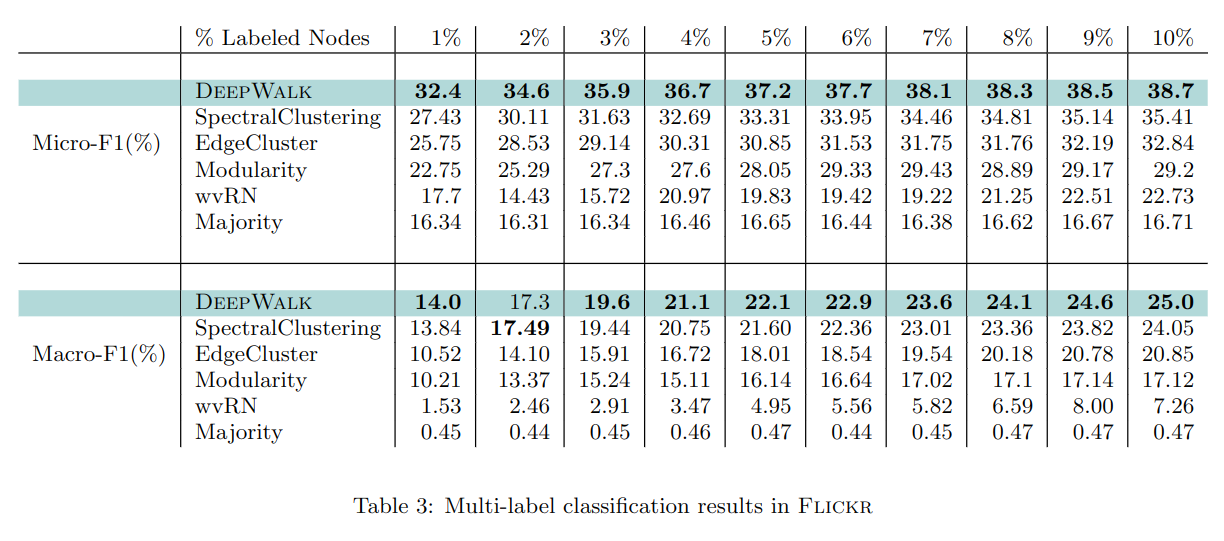
6.1.3 YouTube
YOUTUBE 网络比其它网络大得多,频聚类和模矩阵无法满足这样的计算量。这种网络也更接近现实世界。使用 1%-10% 比例标注。
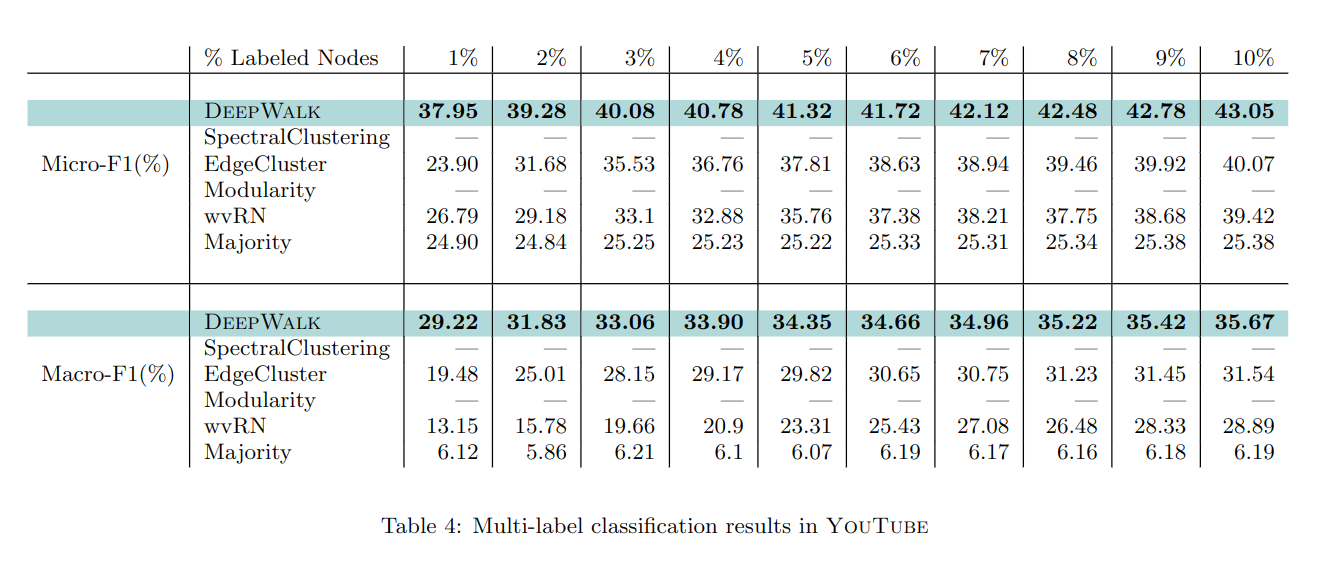
可以看到它在少量标注时明显优于其它算法。
综上,文中方法对于多分类任务,在网络大,稀疏,标注少的情况下效果都很好。
6.2 灵敏度参数
图 -5 展示了参数对分类任务模型的影响。
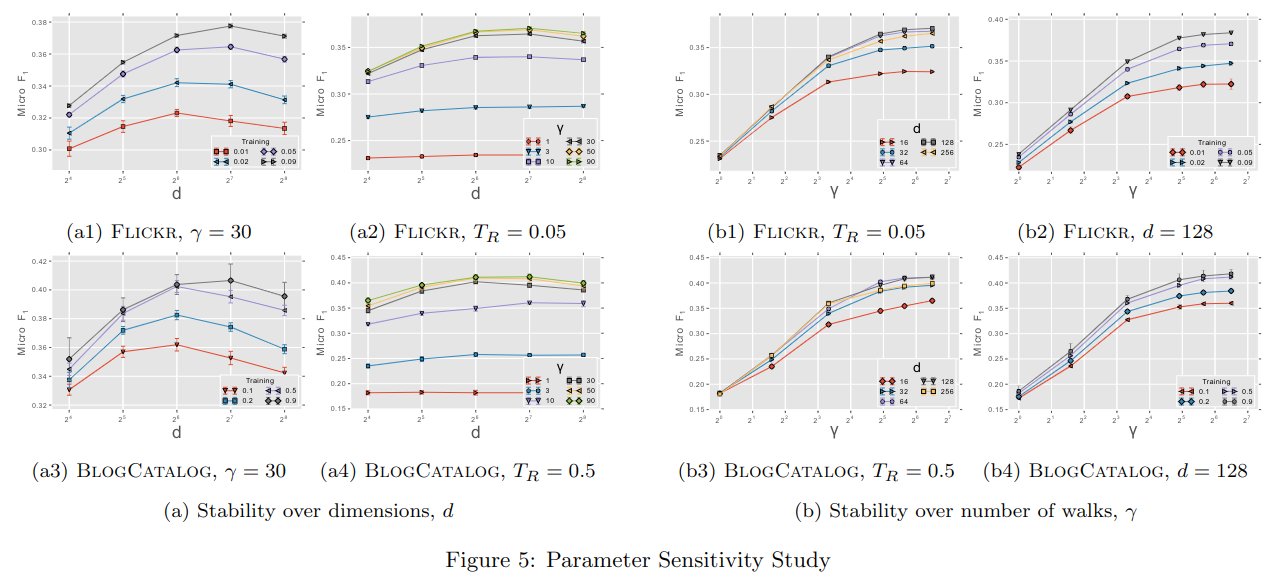
6.2.1 维度影响
其中左边展示了不同输出维度的影响,其中 a1 和 a3 用不同颜色展示不同的训练比率,在两个数据集中结果相似:模型的最优维度依赖于训练样本数。a2 和 a4 不同颜色展示了不同游走次数γ,两图都在γ=30 时性价比最高;虽然 FLICKR 比 BLOGCATALOG 边多一倍,但γ取值不同时,两张图很相似。
这说明文中方法可适应不同大小的网络,且模型表现依赖于游走次数,维度取决于训练样本量。
6.2.2 采样率影响
右图展示了不同游走次数的影响,b1,b3 展示了不同输出维度,b2,b4 展示不同训练样本,情况基本一致,γ对结果有显著影响,而在γ>10 之后再增加次数,效果提升就不太明显了。这说明只需要少量游走,就可以学到节点的表征。
