论文阅读_可扩展特征学习Node2Vec
介绍
英文题目:node2vec: Scalable Feature Learning for Networks
中文题目:node2vec:面向网络的可扩展特征学习
论文地址:https://arxiv.org/abs/1607.00653
领域:图神经网络,知识表示
发表时间:2016
出处:KDD
被引量:6181
代码和数据:http://snap.stanford.edu/node2vec/
参考其它翻译:【论文笔记】node2vec
说明
- 一切皆可 vector
- 图神经网络经典必读第一篇
读后感
(看完题目、摘要、结论、图表及小标题看完,约 30 分钟)
针对问题:自动学习图中结点和边的特征表示
目标:更好地表征图中的节点:兼顾同质性和结构等价性。
结果:在多领域与 SOTA 模型对比,展示算法有效性,可在复杂网络中生成任务无关的表征。
方法:note2vec 框架,优化随机游走算法,结合深度优先和广度优先两种游走方式,用参数设置游走方式的选择,从而提升效率。
精读
(核心章节:读 + 整理:3 小时)
摘要
如果想使用机器学习算法对图中节点和边建模,需要自动学习对图中元素的描述以替代手动对图的特征工程。
文中提出 node2vec 框架,学习对图中节点的连续性特征的表示。将节点映射到低维空间,使图中相邻节点相似性最高。文中设计了一种有偏随机游走过程,核心在于加入有弹性的领域探索方法来增强特征的表达能力。
在多分类和连接预测任务中对比了 node2vec 与 SOTA 模型,展示出文中方法在复杂网络情况下,可有效地学习任务无关的表示。
……
3. 特征学习框架
设 G=(V,E),其中 G 为图,V 是节点,E 是边。设 f 为 V->\(R^d\) 映射函数,将节点 V 映射成特征表示 R,d 是特征维度。对于每个节点 u∈V,定义 Ns(u) 为使用采样策略 S 得到的节点 u 的邻居。
目标是找到映射 f,以最大化节点 u 的邻居是 Ns(u) 的对数概率。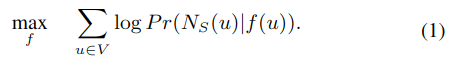 为了简化问题,做以下假设:
为了简化问题,做以下假设:
- 条件独立假设:假设节点与其各个邻居之间的关系相互独立
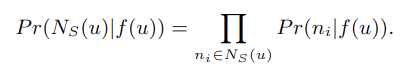
- 特征空间中的对称性:节点与其邻居的关系是对称的。
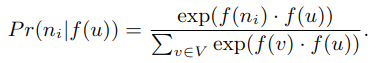
基于上述两个假设,公式一可简化成:
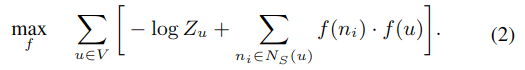
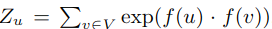
当网络很大时,使用负抽样来逼近它;并使用随机梯度上升法来优化模型参数。
特征学习方法使用自然语言处理中的 Skip-gram 方法。
经典搜索策略
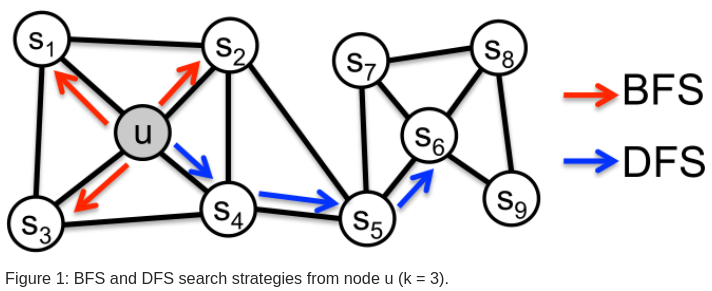
常见两种采样策略:
- 广度优先 (BFS)
邻域由与它直接连通的节点组成,如上图所示,当邻居数据 k=3 时,BFS 采样节点 s1,s2,s3。
- 深度优先 (DFS)
邻域由距离源节点越来越远的顺序采样的节点组成,如上图中的 s4,s5,s6。
同质性和相似结构:
- 同质性
同质网络中各个节点往往是相互连通的,如上图中的 u 和 s1 就属于同质网络。
- 结构相似
当节点有类似的网络结构时,这些节点可能充当相似角色,比如上图中的 u 和 s6 具有结构相似性(看起来像节点中的 hub)。需要注意的,结构相似的网络可能并不相连,它们可能出现在网络的不同位置。
另外,同质性和结构相似性往往在网络中并存。
不同的采样策略决定了节点的特征表示,基于 BFS 的嵌入方法与结构相似性相关,它可以找到微观局部的邻居,当目标节点起到桥接或 hub 作用时,通过直接邻域就可以发现。用 BFS 只能探索图中比较少的区域。相对来说,DFS 可以探索更大区域,它反映了邻域的宏观情况,即同源性。它不但需要推断节点间依赖性,还要推断精确的关系,这相对困难,另外,深度优先涉及更远更复杂的依赖,且一般来说距离越远,相关性越小。
3.2 node2vec
文中提出了一种弹性的邻域采样策略,兼顾深度和广度。
3.2.1 随机游走
对于节点 u,先设定游走的步数 l,用 ci 表示第 i 步游走的分布,比如第 0 步时 c0=u。
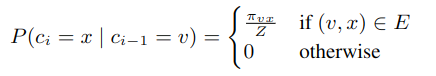
其中πvx 是节点 v 和 x 之间的转移概率,而 Z 是归一化常数。
3.2.2 有偏探索
最简单的方法是根据边的权重采样下一个节点,但这样无法兼顾网络结构以及不同的邻居类型。另外,还需要结合 BFS 和 DFS,而非二选一。
文中使用了 p,q 两个参数,如图所示:上一步从 t 到 v,目前处于节点 v,此时计算边的转移概率πvx:
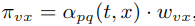
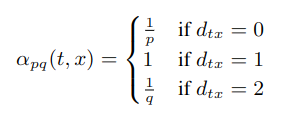
其中 wvx 是图中边的权重,dtx 是从 t 到 x 的最短路径距离(注意这里指的是 t 和 x 的距离,不是 v 和 x 的距离)。
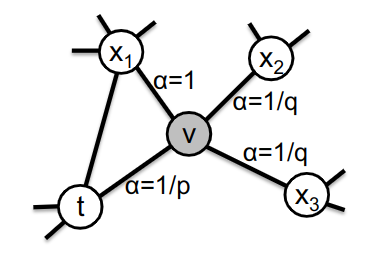
如图所示,参数 p 和 q 控制着游走的距离以及近邻数。
返回参数 p:p 控制是否返回 t 节点,p 较大时,不容易返回 t 节点,它鼓励了模型向外探索,并避免了两跳冗余;当 p 较小时,则使距离足够短,使表示具有微观性。
向内/向外参数 q:q 允许选择探索向内或向外的节点,当 q>1 时,随机游走倾向回到 t,使表示具有微观性;当 q<1 时,则倾向广度优先。与完全的深度优先不同,这里只考虑了两步。
相对于单纯的深度或广度优先,随机游走在空间和时间上都更加高效。
3.2.3 node2vec 算法

PreprocessModifiedWeights 根据参数 p,q 和图 G 生成转换概率;外循环表示生成 r 次随机游走;内循环对于每个节点 u,用 node2vecWork 生成随机游走,最后使用随机梯度下降 SGD 优化模型参数。
函数 note2vecWork 用于生成每个节点的游走,遍历每种可能的游走长度 l,将当前节点 curr 设为最后添加的节点,找到它所有的邻居节点,然后根据转移概率π进行有偏采样,得到邻居 s 并将其加入 walk。
最终由三步构成:计算转移概率、模拟随机游走、使用 SGD 优化。
3.3 学习边的特征表示
node2vec 提供了半监督的节点特征学习方法,有时我们对于节点间的关系更感兴趣,比如链接预测:两个节点间是否存在连接,随机游走方法可将节点的表示扩展成边的表示。
假设两个节点 u 和 v,其特征向量为 f(u),f(v),则两个节点的关系被表示为 g(u,v)。无论 u 与 v 之间是否有边存在,都可以用这种方法表示(存在边为 true,不存在为 false)。还有一些方法也可以用于表示边,如下表所示。
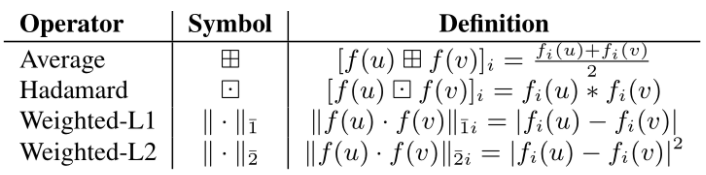
图 3 描述了节点的关系,上图为同质化,下图为结构一致性。

