论文阅读_广义加性模型
英文题目:Intelligible Models for Classification and Regression
中文题目:可理解的分类和回归模型
论文地址:https://www.doc88.com/p-41099846725043.html
领域:模型可解释性,广义加性模型,机器学习
发表时间:2012
作者:Yin Lou,Rich Caruana(模型可解释性大佬),康耐尔大学,微软
出处:KDD
被引量:256
代码和数据:https://github.com/interpretml/interpret
阅读时间:220819
读后感
加性模型的准确性优于线性模型,差于梯度决策树和深度学习模型.它在模型精度和可解释性间取平衡.其核心原理是针对单个特征建立模型(可以是非线性模型),然后把这些复杂模型加在一起形成最终模型.本文描述了具体实现方法.
介绍
复杂模型虽然预测精度高,但可解释性较差,因为很难判断单个特征在复杂模型中的贡献度.本文目标是建立尽量准确且可解释的模型,让用户可以理解每个特征的贡献度.使用广义加性模型(GAMs)方法,其核心算法如下:
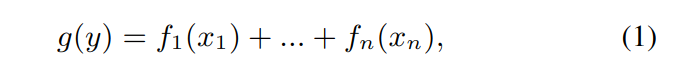
将 g 称为 link 函数,f 称为 shape 函数,g 和 f 可以是任何函数,比如非线性函数,对于单个特征建模 f,f 可以有很高的复杂度,但特征之间组合比较简单,只能是叠加关系.
比如下式就是一个加性模型的示例:
\[ y=x_1+x^2_2+\sqrt{x^3}+log(x_4)+exp(x_5)+2sin(x_6)+\epsilon \]
对应的每个特征影响如图 -1 所示,可以分别看到每个特征对 y 的影响.
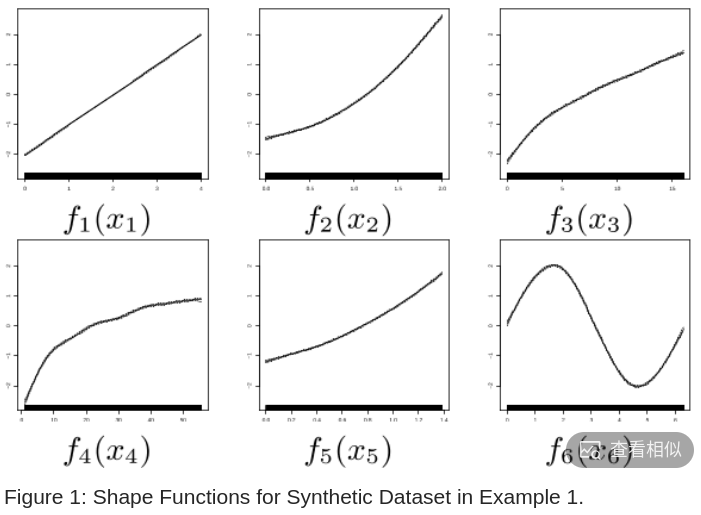
每个 shape 函数都可以是非线性的,这也是加性模型效果优于线性模型的原因.表 -1 展示了各种模型的基本公式:

方法
设数据集中有 N 个实例,每个实例有 n 个特征{xi1...xin},标签为 yi.目标是构建函数 F(x),最小化损失函数 L(y,F(x)).
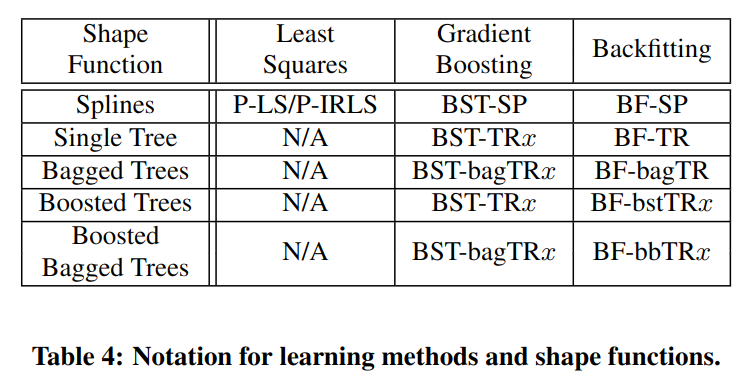
具体实现方法涉及两个维度,对于单特征训练的 shape 模型,一般使用样条函数或者树模型(图 -4 中的纵向);对于 shape 模型的组合训练方法(图 -4 中的横向),即如何训练整体模型,则可选用最小二乘法,梯度提升和回修法.
shape 函数
文中提到的 shape 函数有样条函数和集成树函数,所有 shape 函数只涉及单个特征作为输入.
样条函数
样条是一种特殊的函数,由多项式分段定义.比如三次样条中的每一段都由三次多项式表示,且整体是一条光滑的曲线,三次多项式形如:
\[ y=a_i+b_ix+c_ix^2+d_ix^3 \]
文中使用了设置维度为 d 的回归样条函数:
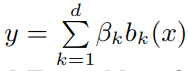
树和集成树模型
使用二叉树和集成二叉树方法,用叶节点个数可描述树的复杂度.树模型的每个分叉是对同一特征的不同值范围进行切分.支持的树包括:Single Tree,Bagged Trees,Boosted Trees,Boosted Baaged Trees.后面的实验中将首字体作为其方法的缩写.
训练整体模型
用以下方法训练整体模型,用最小二乘训练样条函数,用梯度提升和回修训练树模型.
最小二乘法
最小二乘法可以很好的训练线性模型,这里将 bk(x) 看成特征,训练拟合参数 Bk.另外,还加入了平滑系数 λ.实验中将该方法称为惩罚最小二乘,记作 P-LS.对于逻辑回归问题,将样条被简化为用不同的基拟合逻辑回归,方法称为惩罚迭代重加权最小二乘,记作 P-IRLS。
Boosting 梯度提升法
在每一次迭代中,循环地依次训练所有特征,具体方法如下:

- line 1: 将每个 shape 函数初值设为 0
- line 2: 一共 10 次迭代:M=10
- line 3: 遍历所有特征:假设一共三个特征 n=3
- line 4: 这里构造了一个数据集合 R,对于所有实例 i=1...N,其自变量是实例中是第 j 个特征 xij,因变量是将每个实例 i 代入当前所有 f 后(有几个特征就有几个 f,这里用 k 表示特征数)计算预测值,然后计算预测与真值 y 的残差.
- line 5:学习 Shape 函数 S,利用第 j 个特征 x,训练 S(x) 用于拟合 R,之所以是 Boosting,是因为它拟合的不是 y 本身,而是拟合残差
- line 6:利用拟合的残差函数 S 调整更新第 j 个特征的拟合函数 fj
Backfitting 回修法
回修法是之前拟合加性模型的主流方法,它与梯度提升方法非常类似,差别在伪代码的第 4 行和第 6 行,在第 4 行,回修法的 fk 不包含其本身对应的第 fj;而第 6 行,直接用 S 替换 fj.对比可以看出梯度提升拟合的是残差,而回修法拟合的是 fj 本身,因此,随着数据不同,回修的波动可能相对较大,最终可能难以收敛.
实验
图 -3 对比了梯度提升和回修方法对回归 (a,b,c) 和分类 (d,e,f) 的建模效果,可以看到,当叶节点过多时,在训练集中效果好,但在测试集上效果差,回修法效果相对不稳定.
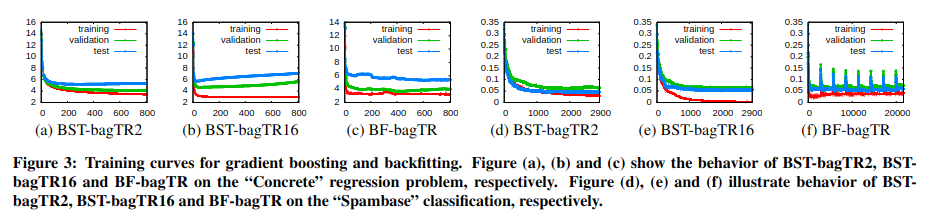
图 -5 对比了使用不同 Shape 函数的效果,第一行样条函数由于追求拟合曲线的平滑,在数据较少的位置拟合效果较差,这可能是由于样条过于平滑,学不出细节.相对来说第二行的树模型效果更好.
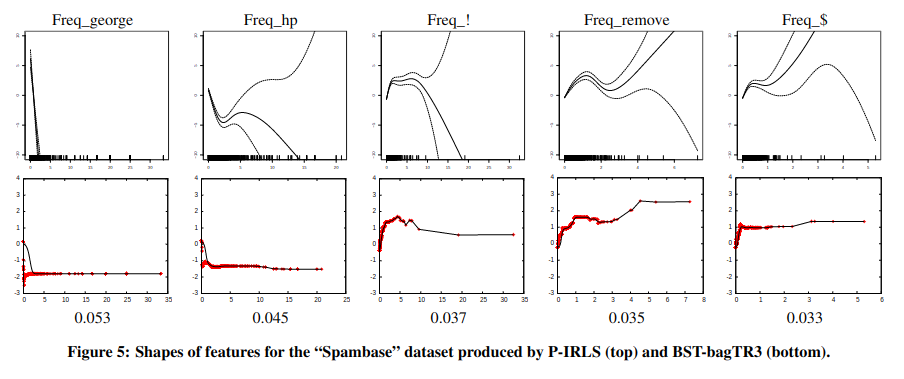
表 -5 展示了主实验结果,这里使用了 6 个回归数据集,从实验结果的均值可以看到,复杂模型效果最好,加性模型中,BST-bagTRX 效果最好,它是梯度提升的 Bagging 树,X 表示随机设置叶节点数.
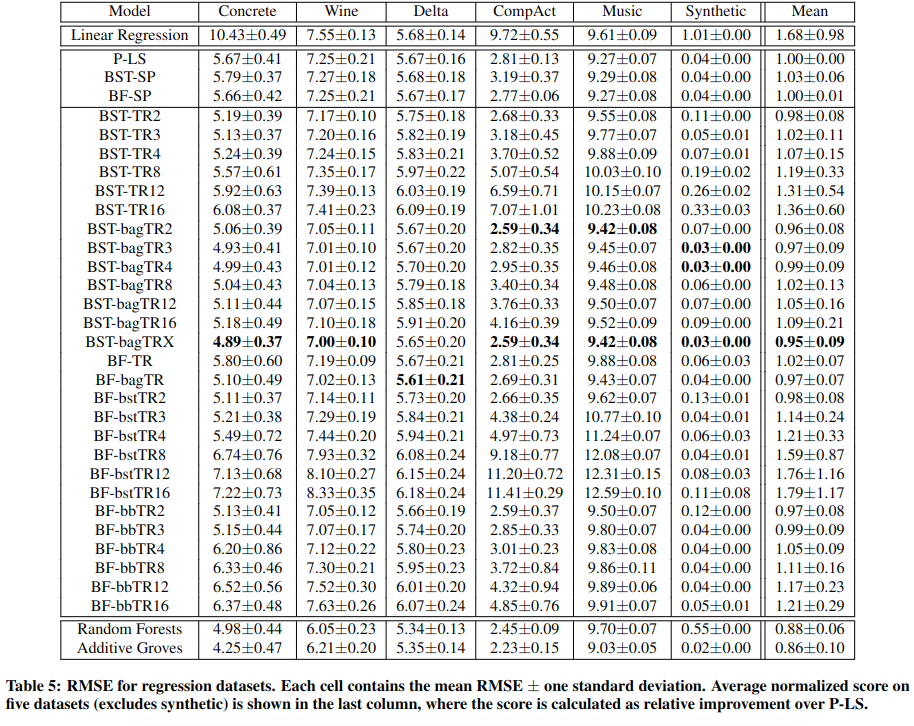
比较有意思的是,在 BST-bagTR 类中,叶节点 2-4,效果最好,这可能是由于叶节点太多可能造成过拟合.
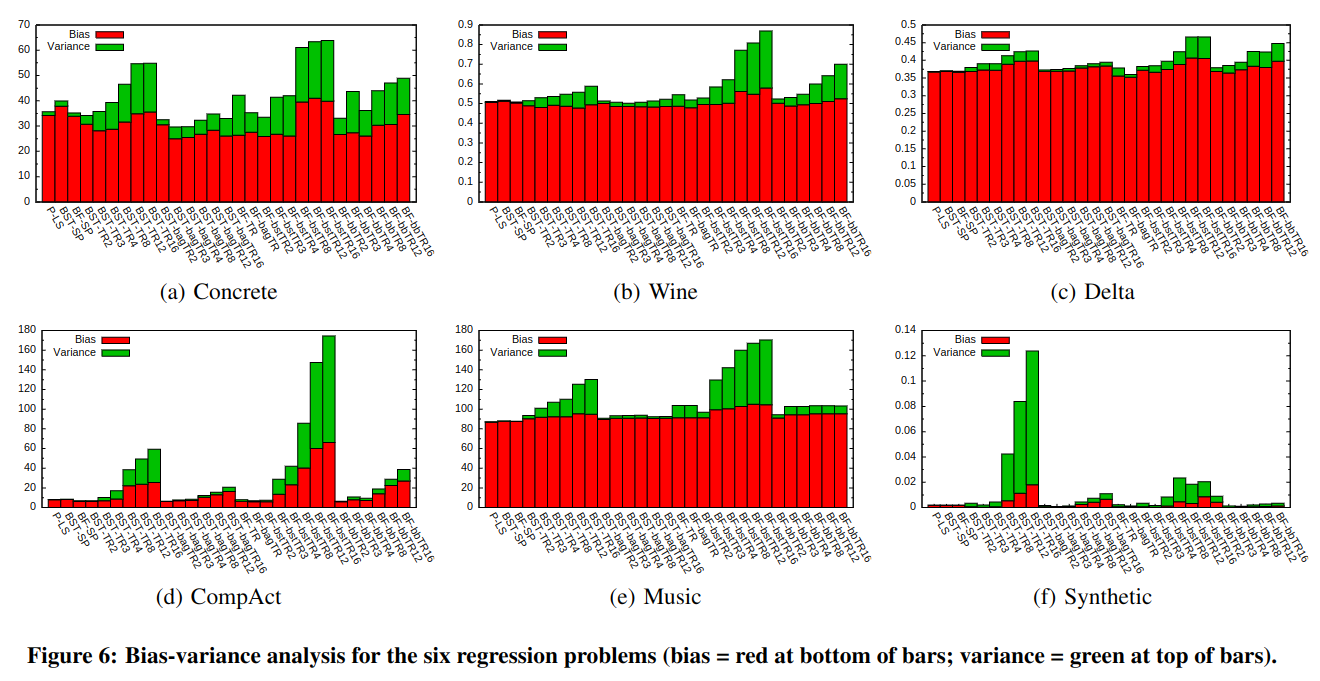
图 -6 展示了回归中各个模型的偏差和方差,偏差描述了模型预测结果和实际 y 之间的差异,方差用于评价子学习器学出结果的一致性,以评价稳定性(常用交叉验证的方法测量方差).可以看到对于所有数据集,位于中间偏左的梯度提升 + 树模型效果都最好.
扩展阅读
GA2M
Accurate Intelligible Models with Pairwise Interactions
是同一作者写的另一篇基于 GAM 的优化,将基于单个特征的加性模型扩展为基于特征组合的加性模型.核心公式如下:
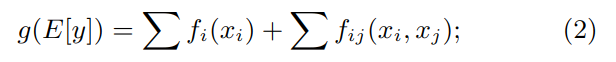
其核心方法在于如何选择和优化特征组合,实验证明在有些情况下比 lightgbm 更好.
实际使用
1 | import numpy as np |
注意:"f" 和 "s" 是两个重要的概念,"f" 指的是预测变量与响应变量之间的非线性关系。"s" 指的是预测变量与响应变量之间的线性关系。其中的参数指对哪一个变量操作,这里 x 只有一个变量,所以都是针对 0 操作。
