有些资产，看起来每天都很稳，涨得不快，却总在某一次下跌中把之前的收益一把抹掉；
有些资产，长期不动甚至让人怀疑人生，但一旦启动，往往在少数几天决定成败。

我们常用“波动大不大”来判断风险，但同样的波动率，带来的体验和结果可能完全不同。
真正的差别，往往不在“波动有多大”，而在于——收益是慢慢给你的，还是一次性拿走的。

偏度和峰度，正是用来回答这个问题的量化工具。

1 概述

偏度（Skewness） 和 峰度（Kurtosis） 是两个不同的统计指标，用来描述数据分布的不同特征：

指标 含义 判断标准
偏度 (Skewness) 分布的对称性（左右倾斜） > 0: 右偏；< 0: 左偏；≈ 0: 对称
峰度 (Kurtosis) 分布的尖锐程度（尾部厚度） > 0: 更尖锐，尾部更厚；< 0: 更平坦

2 偏度

偏度：描述 " 歪斜 " 程度

  • 右偏 (正偏度)：长尾在右边，更容易出现大涨，即 Skewness > 0
  • 左偏 (负偏度)：长尾在左边，更容易出现大跌，即 Skewness < 0

偏度的范围是 -∞ 到 +∞，但实践中大多数情况下在 -3 到 +3 之间。

判断标准：

偏度值范围 含义 投资意义
> 1 或 < -1 高度偏斜 分布极度不对称，趋势明显，重点关注
0.5 ~ 1 或 -1 ~ -0.5 中度偏斜 分布有明显倾向
-0.5 ~ 0.5 接近对称 分布基本对称，涨跌相对均衡
-0.2 ~ 0.2 略偏或对称 参考你代码中的阈值

3 峰度：描述 " 尖锐 " 程度

峰度（kurtosis）衡量分布“两边厚不厚、尾巴长不长”，不是看山尖不尖，而是看“极端情况出现的概率”。SciPy 中 stats.kurtosis() 默认使用的是超峰度（Excess Kurtosis），公式是：

(四阶中心矩 / 方差²)-3

其中： - 方差：二阶中心矩，是“差多少”的平均 - 四阶中心矩：是“差多少的四次方”，所以特别强调尾部，偏得越远，贡献越夸张 * 减 3：因为正态分布的峰度是 3，所以减掉让“正常分布的 kurtosis = 0”

高峰度 (Kurtosis > 0)：分布尖锐，极端值更多，更容易出现 " 黑天鹅事件 " 低峰度 (Kurtosis < 0)：分布平缓，数据分散均匀，极端值较少

判断标准：

超峰度值 含义 风险特征
≈ 0 正态分布 正常风险分布
> 0 (如 1.x, 5.x) 尖峰厚尾 极端事件更多，黑天鹅风险大
< 0 平顶分布 数据分散均匀，极端值少
很高 (如 30.x) 极度尖峰 巨大波动浓缩在小范围，风险集中

4 方法

1
2
3
4
5
# 偏度 → 判断涨跌倾向
skewness_returns = stats.skew(daily_returns) # 正值=容易大涨，负值=容易大跌

# 峰度 → 判断风险尖锐度
kurtosis_returns = stats.kurtosis(daily_returns) # 高峰度=极端波动多，风险集中

5 示例

这是一个左偏，且峰度大的示例：它的急跌更多

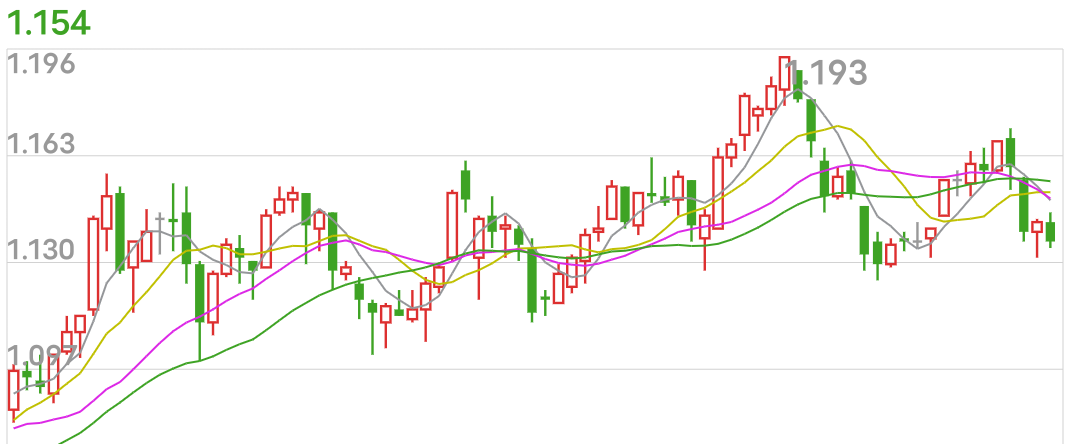
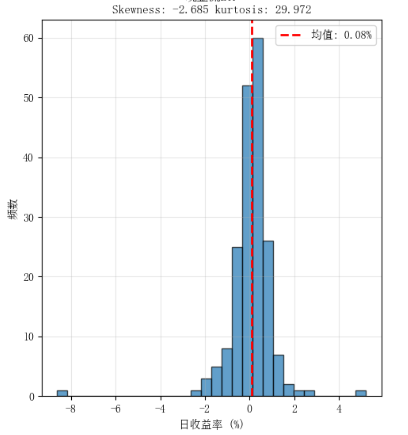这是一个右偏，峰度也较大的示例：它的急涨更多

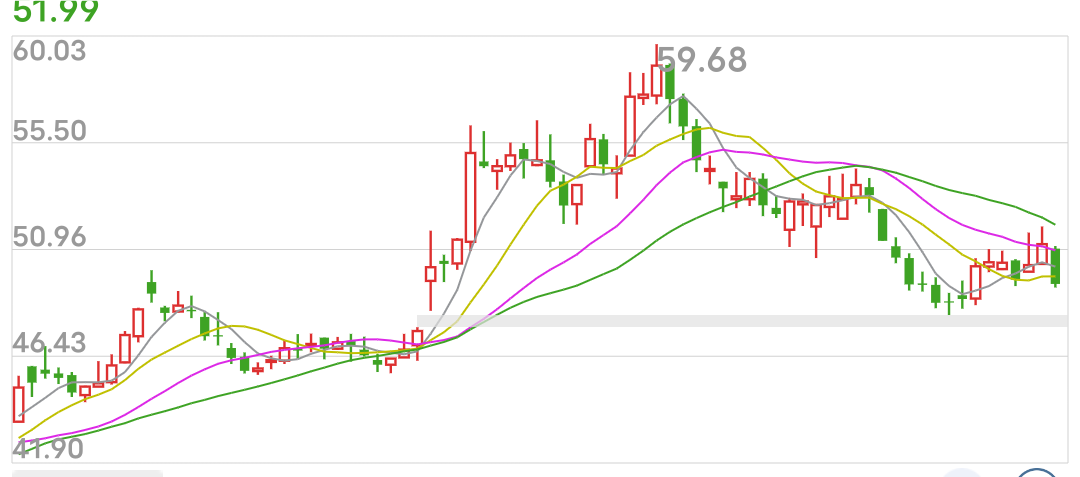
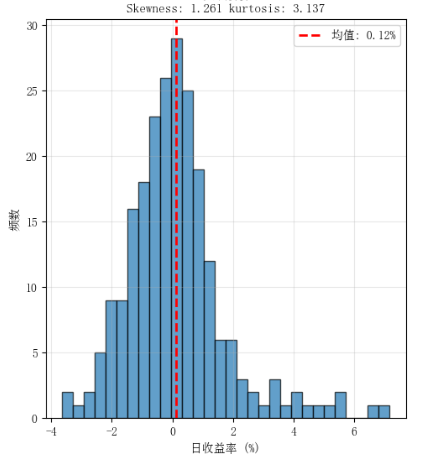## 6 实战中应用

  • 右偏 + 高峰度：容易大涨但偶有大跌 → 高风险高收益
  • 左偏 + 高峰度：容易大跌且极端事件多 → 谨慎应对
  • 接近对称 + 低峰度：涨跌均衡且稳定 → 风险较小

从日收益率分布看，大部分ETF偏左：上涨缓慢（个股上涨被摊平），但市场恐慌时易集体急跌，买入可慢慢布局，但卖出需果断，不要因“平稳上涨”而大意。强势个股更右偏：容易突然拉升，买要果断，卖则可适当给趋势留余地。

从心理层面看，更需要警惕的是负偏分布下的缓涨急跌：它往往让人逐步放松警惕，而真正的风险集中在少数几次大跌中，一次就可能吃掉多年收益。而正偏资产的难点不在于暴跌，而在于收益高度依赖少数时刻：在行情迟迟未出现之前，长期的小亏、小赚或横盘，会不断考验持有者的耐心和信念，很多人往往在真正的大涨来临前选择离场。

可以说：

  • 负偏的敌人：风险管理
  • 正偏的敌人：耐心和信念

另外，需要注意，偏度并非固定属性，而是随时间动态变化：行情好时，ETF也可能右偏；个股高位松动时则可能左偏。偏度应被视为情绪信号，用于调整买卖节奏，而非给资产贴标签。